GSoC Blog: Second Evaluations


Hello Everyone! So I am here to present my work and contributions I made before the second evaluation in Google Summer of Code 2020. The project is under the supervision of The Julia Language.
Parallel Extrapolation Methods
After discussing with my mentors about what to do next, I chose to pick my of the sub-project: Parallel Extrapolation Methods. We already had an implementation of them, but they haven’t optimised add benchmarks were not up to the mark. They are broadly divided into Explicit and Implicit Methods. Since these algorithms were new to me, I quickly skimmed through Hairer II about these methods and learnt about them. The Extrapolation methods estimate a higher order of solutions through computing the same t solution from reduced step-sizes. These are VSVO methods which provide order variation from 2 to 12 with internal discretisation. I must say, Hairer II is one of the most comprehensive and lucid books written about computation methods!
Explicit Methods
Our native Julia methods are all about speed and optimisations. I started diagnosing the explicit methods first to get a better understanding of the codebase. Our codebase was loosely based on the Hairer book and was more about one of the contributor’s thesis whose MVP was barycentric extrapolation. Rather than using conventional Aitken Nevile’s Algorithm with O(N2d) operations, the barycentric extrapolation reduces it to O(N*d) . It was an added advantage against native Fortran ODEX solvers.
While they were quite optimised, I resolved some internal discretisation issues which reflected in the benchmarks positively. I also extended the solver API to include sequence factor which helps user to adjust accuracy with a trade-off in time complexity according to the scope of the problem. The multi-threaded version often proved sometimes better which parallelised internal discretisations and f-evaluations.
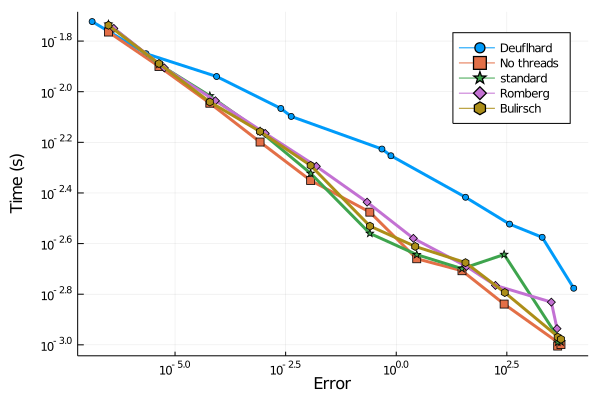
Implicit Methods
Although Explicit Methods are fast and easy to implement, they are not suited for Stiff problems. Since most of the problems we encounter in nature are helplessly Stiff, we need advanced solvers to solve it. One of them is Implicit Extrapolation methods. The basis algorithms for these solvers are Implicit Euler Method and Implicit Midpoint Method. The main highlight of these methods is that they are semi-implicit, which translates to not solving the equation using quasi-newton iterative schemes. The “Implicitness” is models by the Jacobian Matrix or most importantly the W matrix, I-hJ, adapted from the works of Lawson-Euler and Bader-Deuflhard. Therefore these methods theoretically are quicker than traditional implicit methods coupled with accuracy tuning using variable order. We have two different adaptive schemes, one which is based on Deuflhard’s initial work (1973) and new Hairer-Wanner scheme discussed in Hairer II.
Problems
- Although the existing implementation passed basic linear and regression tests, the algorithm didn’t simply scale to Stiff problems like the Van Der Pol Oscillator, ROBER etc. because of the overflow. Due to Julia’s awesome BigFloats which provided infinite precision, I was able to run these solvers and check their dense solutions.
- After checking the solution, there were some perturbations at various time-stamps which implied the solver wasn’t able to account the stiffness in that time domain.
- The work accounts simply for how many significant computations our algorithm make in a particular order. The work calculation and adaptive time-stepping weren’t compatible with Implicit solvers.
- The number of Function evaluations. Jacobian and W evaluations and linear solvers affect the speed of the solver to a great extent. I found that these could be optimised up to 4x-8x times.
Solutions and Fixes
- I fixed it by checking the divergence of successive internal iteration as suggested by Deuflhard. It immediately solved the Float overflow and increased the solver speed up to 10x times.
- Implemented Gragg’s smoothing, which is an estimation of solution at t with neighbouring values which literally ‘smoothed’ the perturbations.
- Rectified the work calculation which affected the time-stepping strategy positively and our solver became faster.
- I split the Jacobian and W matrix calculation and optimised them to calculate when it was modified.
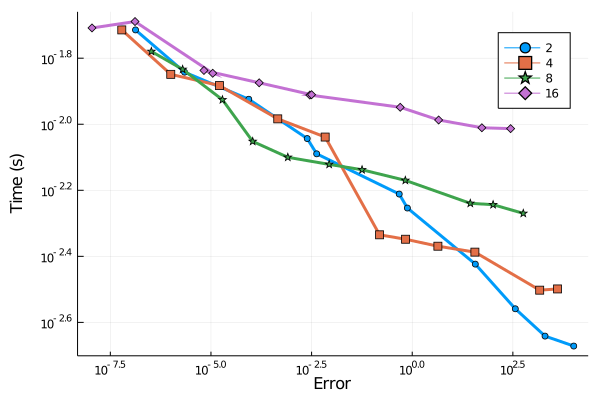
Multi-threading
The highlighting point of these solvers is the multi-threading compatible. These methods have arguments for max_order, min_order, and init_order on the adaptive order algorithm. Threading denotes whether to automatically multithread the f evaluations and J/W instantiations+factorizations, allowing for a high degree of within-method parallelism. We recommend switching to multi-threading when the system consists of more than ~ 150 ODES.
Benchmarks
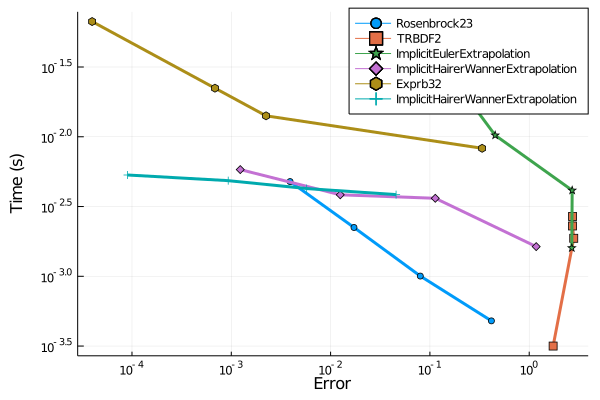
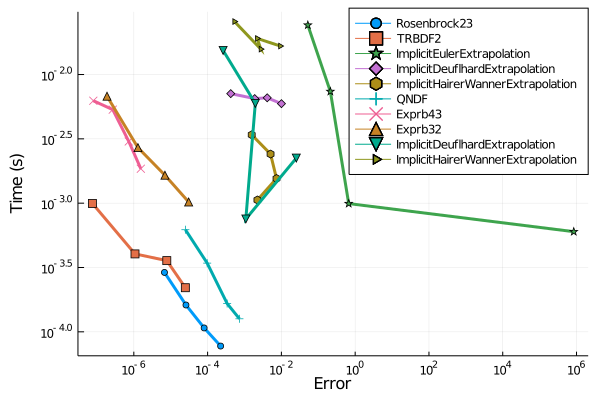
List of Contributions
OrdinaryDiffEq.jl
| Description | Pull Requests | Current Status |
|---|---|---|
| Add sequences for Implicit Euler Extrapolation | #1199 | Merged |
| DEStats update in extrapolation method and fixes | #1200 | Merged |
| Sequence factor option in explicit extrapolation algo | #1202 | Merged |
| Recalculating Jacobian in Internal Discretisation | #1203 | Merged |
| Update T cal in adaptive step-sizing Extrapolation | #1208 | Merged |
| Update Work Calc in Implicit Extrapolation Methods | #1209 | Merged |
| Fix Overflow in Implicit Extrapolation Methods | #1211 | Merged |
| Add Gragg’s Smoothing to ImplicitHW Extrapolation | #1212 | Merged |
| Multi-threading for Implicit Hairer-Wanner | #1213 | Merged |
| Multi-threading for Implicit Extrapolation Methods | #1215 | Merged |
| Update Work Calculation in ImplicitEulerExtrapolation | #1217 | Merged |
DiffEqDocs.jl
| Description | Pull Requests | Current Status |
|---|---|---|
| Broken Eg. in Implicit Euler Extrapolation | #379 | Merged |
| Update Parallel Extrapolation Docs | #388 | Merged |
DiffEqDevDocs.jl
| Description | Pull Requests | Current Status |
|---|---|---|
| Update Benchmarks to DiffEqDevTools | #20 | Merged |
Future Goals
There’s some improvement left in ImplicitEulerExtrapolation, I will try to fix it and optimise them and move to next project after discussion. I would like to also work on general fixes in ODE solvers in OrdinaryDiffEq.jl. Till then, happy coding!